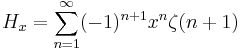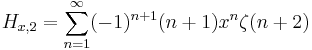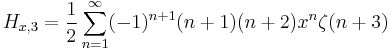Harmonic number
- The term harmonic number has multiple meanings. For other meanings, see harmonic number (disambiguation).
In mathematics, the n-th harmonic number is the sum of the reciprocals of the first n natural numbers:
This also equals n times the inverse of the harmonic mean of these natural numbers.
Harmonic numbers were studied in antiquity and are important in various branches of number theory. They are sometimes loosely termed harmonic series, are closely related to the Riemann zeta function, and appear in various expressions for various special functions.
When the value of a large quantity of items has a Zipf's law distribution, the total value of the n most-valuable items is the n-th harmonic number. This leads to a variety of surprising conclusions in the Long Tail and the theory of network value.
Contents |
Calculation
An integral representation is given by Euler:
The equality above is obvious by the simple algebraic identity below
An elegant combinatorial expression can be obtained for 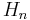 using the simple integral transform
using the simple integral transform 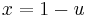 :
:
The same representation can be produced by using the third Retkes identity putting  and using the fact that
and using the fact that 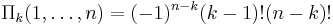 .
.
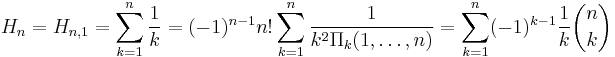
If we use Retkes identity for  in which case
in which case 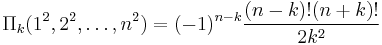 one can have an analog formula for the n-th partial sum of
one can have an analog formula for the n-th partial sum of 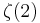
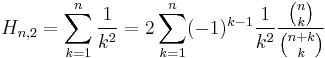
Hn grows about as fast as the natural logarithm of n. The reason is that the sum is approximated by the integral
whose value is ln(n).
The values of the sequence Hn - ln(n) decrease monotonically towards the limit:
(where γ is the Euler–Mascheroni constant 0.5772156649...), and the corresponding asymptotic expansion as 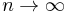 :
:
where  are the Bernoulli numbers.
are the Bernoulli numbers.
Special values for fractional arguments
There are the following special analytic values for fractional arguments between 0 and 1, given by the integral
More may be generated from the recurrence relation 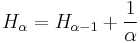 or from the reflection relation
or from the reflection relation 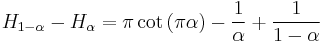 .
.
For every 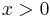 , integer or not, we have:
, integer or not, we have: 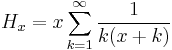
Based on 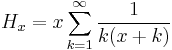 , we have:
, we have: 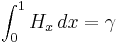 , where
, where  is the Euler–Mascheroni constant or, more generally, for every n we have:
is the Euler–Mascheroni constant or, more generally, for every n we have: 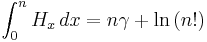
Generating functions
A generating function for the harmonic numbers is
where 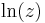 is the natural logarithm. An exponential generating function is
is the natural logarithm. An exponential generating function is
where 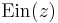 is the entire exponential integral. Note that
is the entire exponential integral. Note that
where 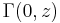 is the incomplete gamma function.
is the incomplete gamma function.
Applications
The harmonic numbers appear in several calculation formulas, such as the digamma function:
This relation is also frequently used to define the extension of the harmonic numbers to non-integer n. The harmonic numbers are also frequently used to define γ, using the limit introduced in the previous section, although
converges more quickly.
In 2002 Jeffrey Lagarias proved that the Riemann hypothesis is equivalent to the statement that
is true for every integer n ≥ 1 with strict inequality if n > 1; here σ(n) denotes the sum of the divisors of n.
The eigenvalues of the nonlocal problem
are given by 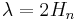 , where by convention,
, where by convention, 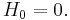
Generalization
Generalized harmonic numbers
The generalized harmonic number of order  of m is given by
of m is given by
Note that the limit as n tends to infinity exists if 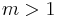 .
.
Other notations occasionally used include
The special case of 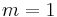 is simply called a harmonic number and is frequently written without the superscript, as
is simply called a harmonic number and is frequently written without the superscript, as
In the limit of 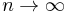 , the generalized harmonic number converges to the Riemann zeta function
, the generalized harmonic number converges to the Riemann zeta function
The related sum 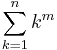 occurs in the study of Bernoulli numbers; the harmonic numbers also appear in the study of Stirling numbers.
occurs in the study of Bernoulli numbers; the harmonic numbers also appear in the study of Stirling numbers.
Some integrals of generalized harmonic are: 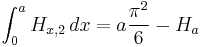
and 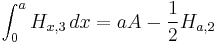 where
where  is the Apéry's constant.
is the Apéry's constant.
A generating function for the generalized harmonic numbers is
where 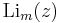 is the polylogarithm, and |z| < 1. The generating function given above for m = 1 is a special case of this formula.
is the polylogarithm, and |z| < 1. The generating function given above for m = 1 is a special case of this formula.
Multiplication formulas
Using polygamma functions we obtain:
or, more generally:
where 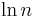 is the natural logarithm.
is the natural logarithm.
For generalized harmonic numbers we have:
where 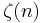 is the Riemann zeta function.
is the Riemann zeta function.
Generalization to the complex plane
Euler's integral formula for the harmonic numbers follows from the integral identity
which holds for general complex-valued s, for the suitably extended binomial coefficients. By choosing a=0, this formula gives both an integral and a series representation for a function that interpolates the harmonic numbers and extends a definition to the complex plane. This integral relation is easily derived by manipulating the Newton series
which is just the Newton's generalized binomial theorem. The interpolating function is in fact the digamma function:
where 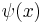 is the digamma, and
is the digamma, and  is the Euler-Mascheroni constant. The integration process may be repeated to obtain
is the Euler-Mascheroni constant. The integration process may be repeated to obtain
Relation to the Riemann zeta function
Some derivatives of fractional harmonic numbers are given by:
And using Maclaurin series, we have for x<1 :
where 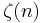 is the Riemann zeta function.
is the Riemann zeta function.
See also
References
- Arthur T. Benjamin, Gregory O. Preston, Jennifer J. Quinn, A Stirling Encounter with Harmonic Numbers, (2002) Mathematics Magazine, 75 (2) pp 95–103.
- Donald Knuth. The Art of Computer Programming, Volume 1: Fundamental Algorithms, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89683-4. Section 1.2.7: Harmonic Numbers, pp. 75–79.
- Ed Sandifer, How Euler Did It -- Estimating the Basel problem (2003)
- Weisstein, Eric W., "Harmonic Number" from MathWorld.
- Peter Paule and Carsten Schneider, Computer Proofs of a New Family of Harmonic Number Identities, (2003) Adv. in Appl. Math. 31(2), pp. 359–378.
- Wenchang CHU, A Binomial Coefficient Identity Associated with Beukers' Conjecture on Apery Numbers, (2004) The Electronic Journal of Combinatorics, 11, #N15.
- Ayhan Dil and Istvan Mezo, A Symmetric Algorithm for Hyperharmonic and Fibonacci Numbers, (2008) Applied Mathematics and Computation 206, 942—951.
- Zoltán Retkes, "An extension of the Hermite–Hadamard Inequality", Acta Sci. Math. (Szeged), 74 (2008), pages 95–106.
This article incorporates material from Harmonic number on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
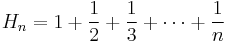
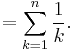
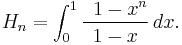
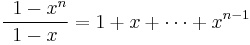
![H_n = \int_0^1 \frac{\,\,\, 1 - x^n}{1 - x}\,dx=-\int_1^0\frac{1-(1-u)^n}{u}\,du=\int_0^1\frac{1-(1-u)^n}{u}\,du=\int_0^1\left[\sum_{k=1}^n(-1)^{k-1}\binom nk u^{k-1}\right]\,du=](/2012-wikipedia_en_all_nopic_01_2012/I/a1c475af31eb45ddefdad44e66b336b4.png)
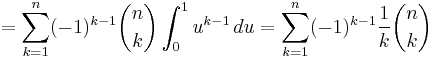
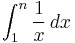
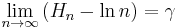
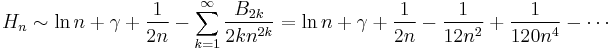
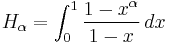
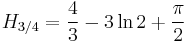
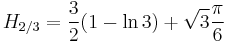
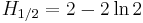
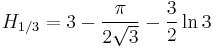
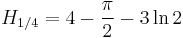
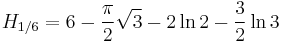
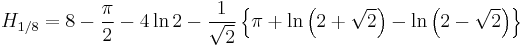
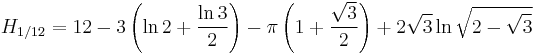
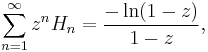
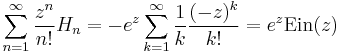
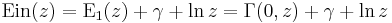
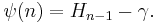
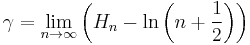
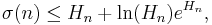
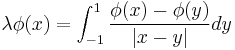
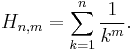
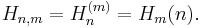
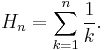
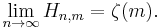
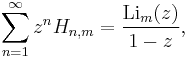
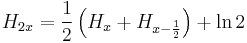
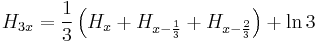
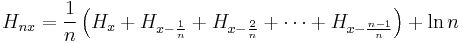
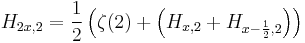
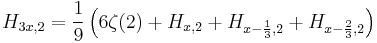
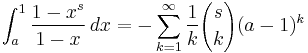
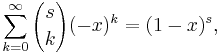
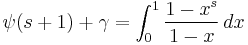
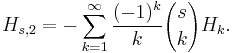
![\frac{d^n H_x}{dx^n} = (-1)^{n%2B1}n!\left[\zeta(n%2B1)-H_{x,n%2B1}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/ce1d807f8f4d1a1f49179fca8e3d40d8.png)
![\frac{d^n H_{x,2}}{dx^n} = (-1)^{n%2B1}(n%2B1)!\left[\zeta(n%2B2)-H_{x,n%2B2}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/0d266ed99ba76f4dce810d9b22a0329c.png)
![\frac{d^n H_{x,3}}{dx^n} = (-1)^{n%2B1}\frac{1}{2}(n%2B2)!\left[\zeta(n%2B3)-H_{x,n%2B3}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/b3f36dd03c83a83081e622c54b4e3395.png)